The block size in open pit mining is often the selective mining unit (SMU) size see previous blog post; however, there are reasons to use smaller blocks, larger blocks and sub-blocks. There is no need for the block size to match the SMU size.
The block size could depend on the data spacing. Blocks smaller than about one quarter the data spacing do not represent additional information. Blocks larger than one quarter the data spacing may create overly smooth representations of the grade. All estimates with widely spaced data are spatially smooth. Even nearest neighbor estimates are spatially smooth - constant grades for large volumes, then abrupt changes. The dispersion of grades on the histogram of estimates, summarized by the variance of blocks, is the measure of smoothing relevant for resources within reasonable production volumes. "Smoothness" here relates to the histogram of block estimates.
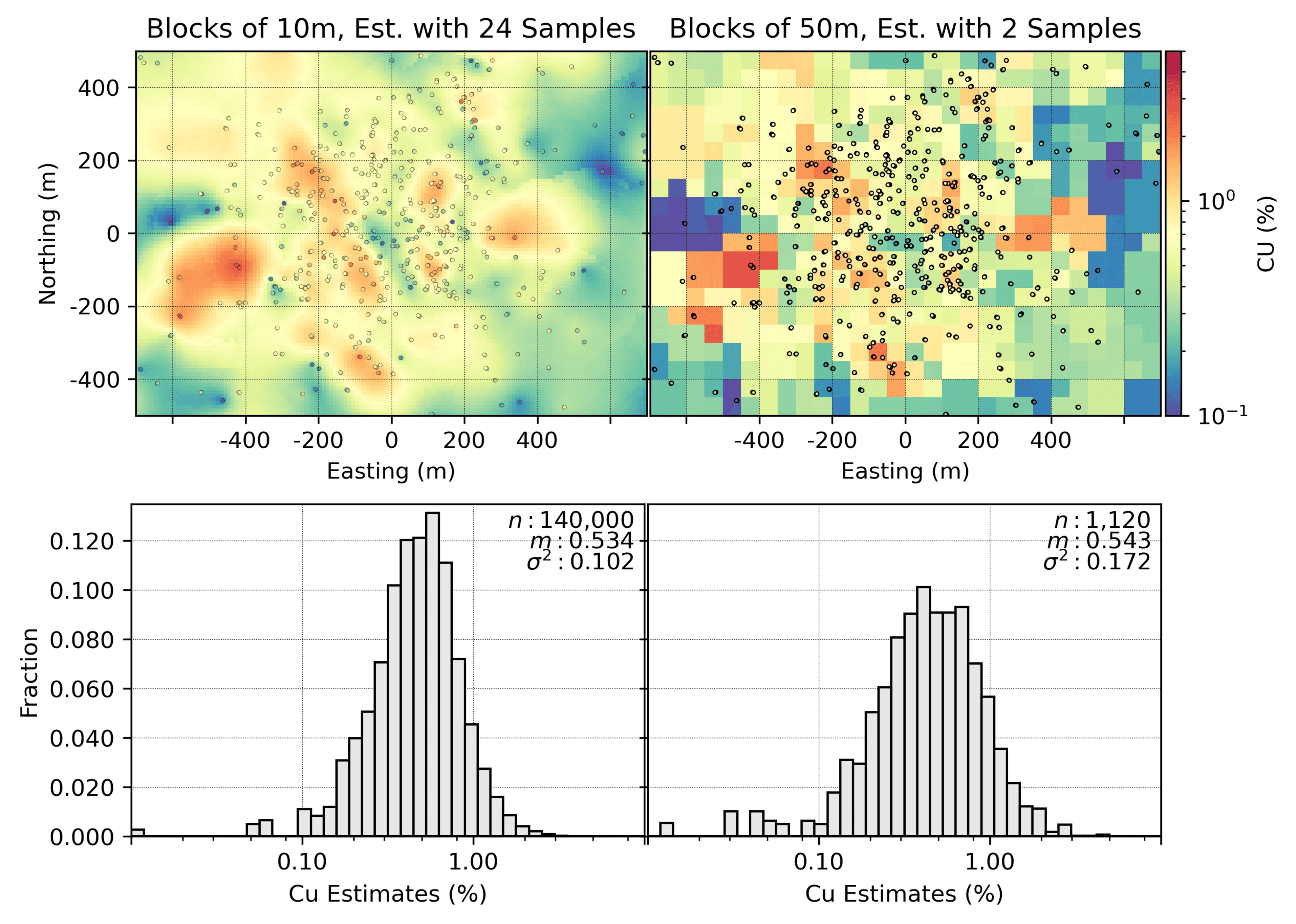
The smoothness of estimates depends more on the estimation search than the block size. Consider the figure below where the small blocks on the left are smooth (variance of 0.102) and the large blocks on the right are not smooth (variance of 0.172). This is due to the kriging search where 24 samples are used for the small blocks and 2 samples are used for the large blocks.
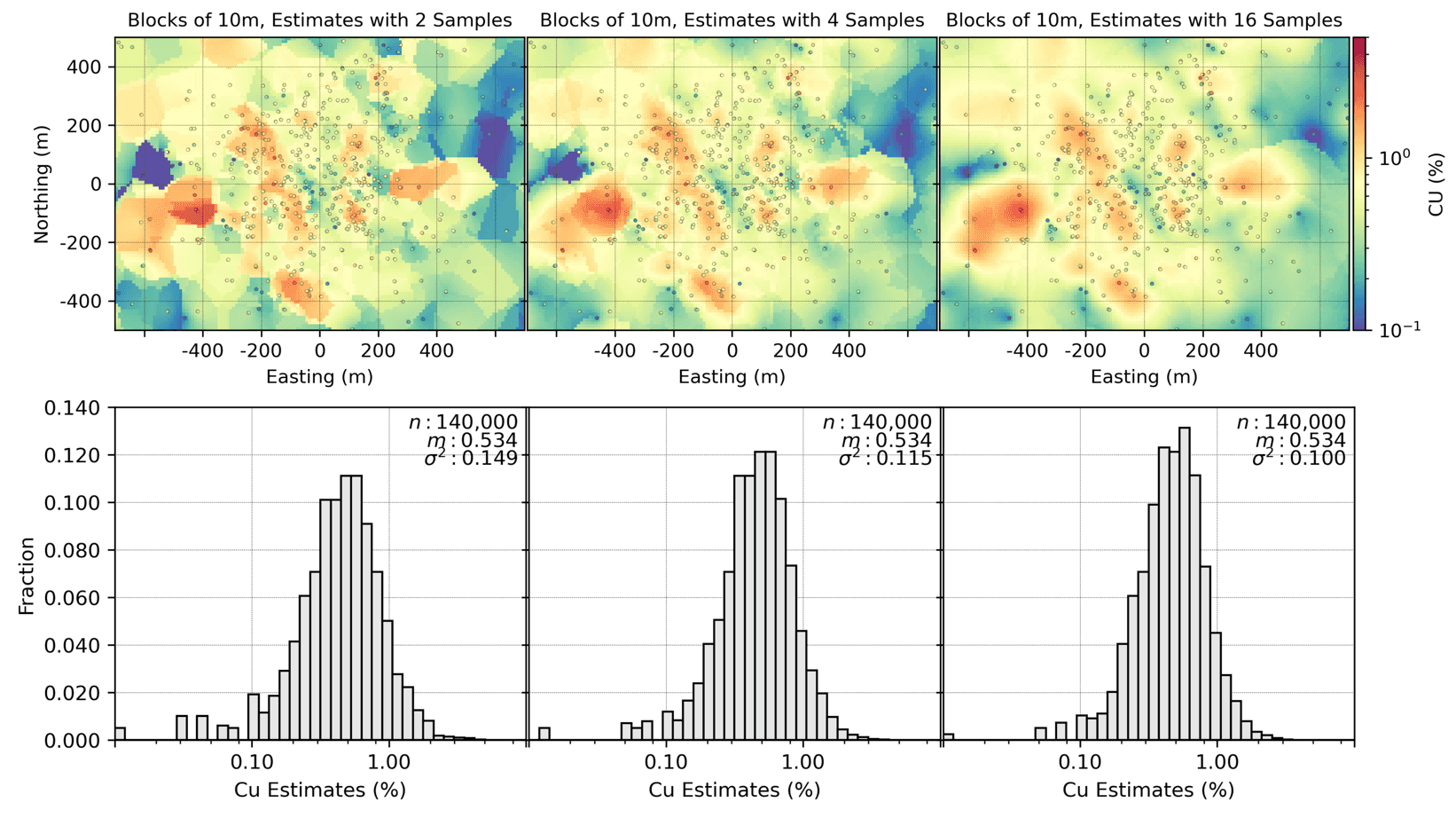
The fact that the smoothness of block estimates depends on the kriging search more than the block size is reinforced by the figures below. At the top, the same sized blocks are estimated with 2, 4 and 16 samples (variance changing from 0.149 to 0.100). At the bottom, square blocks of 2, 10m and 50m are all estimated with 8 samples (variance changing from 0.094 to 0.100). Note that the number of samples in the search have the greatest influence on the variance of the estimates; a 50% change in variance versus a 6% change for the change in block size.
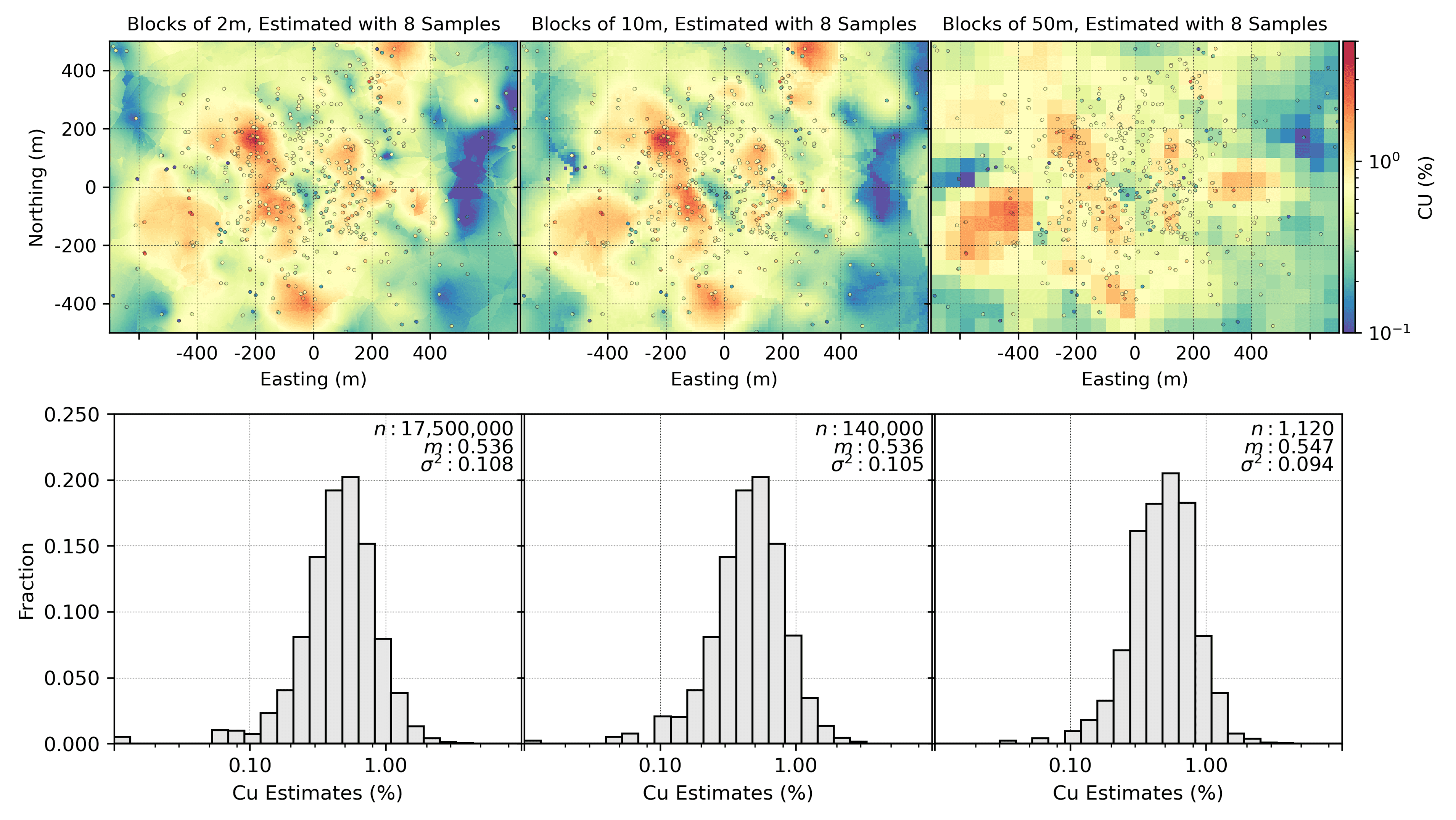
The block size matters. Estimating too-small blocks is computationally inefficient and often not warranted by the data. Estimating too-large blocks does not support mine planning and does not resolve geological contacts very precisely. A reasonable block size should be chosen that is a compromise between computational efficiency and model practicality. There is no need that the block size matches the SMU size, but there is also no need to prefer small blocks or large blocks. Smaller blocks are used for practical engineering and geological considerations, such as allowing pit slopes and geological contacts to be precisely modeled. Larger blocks are used for computational efficiency and to communicate a humble understanding of certainty.
Kriging measures of performance always prefer large blocks. Large blocks have a lower kriging variance, a higher kriging efficiency, higher statistical efficiency, a slope of regression closer to one, less negative weights and less weight to the mean. Despite the theoretical advantage of larger blocks, there is no practical advantage; the estimates of small blocks within a large block are equal to the large block estimate.
Sub-blocks are a practical approach to preserve detail along geological contacts and maintain most of the computational and practical efficiency of large blocks. There is no theoretical advantage to either estimating the parent grade (then assigning to sub-blocks) or estimating sub-blocks directly, but the results can be different with narrow geological domains.
The block size should be chosen reasonably to represent the geological boundaries, capture the information in the sample data and provide support for engineering design. Great care should be taken to tune the kriging search plan including multiple search passes or local search optimization (available in RMSP).
Resource Modeling Solutions provides the software tools and workflows to work with different block models with sub-blocks as required and help resource estimators build the best possible model.



