To impute is to put upon something or someone without their acceptance and, perhaps, without just cause. I always think about the trailer on many emails I receive: If you have received this message in error,… The sender imputes responsibility on the recipient without asking for or gaining acceptance. In statistics and, increasingly, geostatistics we use impute or imputation to describe the process of assigning values where values are missing in a set of data. The main advantage of this methodology is to facilitate techniques that require a full valued data table such as principal component analysis (PCA) or projection pursuit multivariate transformation (PPMT). This can be convenient; however, no technique should be used without due care and discrimination. There are alternatives to imputation. This brings the question about whether to impute or not to impute.
At least one measured value must be available to apply imputation. If all variables of interest are measured at a location, then no special treatment is required. If no variables are available at a location, then it is an unsampled location where all variables must be estimated or simulated. Some collocated data must be available to infer the relationships between the available variables and the missing variables. There may be completely heterotopic data, that is, different data types or data variables that are never measured at the same location; however, cokriging handles this situation. The case of partially missing data is suitable for data imputation.
An important consideration is the nature of missingness. The literature in statistics is confusing at best and misleading at worst. Most of us would not know the difference between missing at random (MAR) and missing completely at random (MCAR). Most of us, however, would ascertain if there is a systematic reason why some data are missing. For example, acid soluble copper may not be assayed unless the total copper exceeds a threshold of importance. Great care is taken to extrapolate relationships beyond the range of observed data in presence of such systematic sampling.
Regarding imputation, a single number cannot be assigned to a missing value with certainty. A single value would be assigned by some form of regression or machine learning and would be too smooth and fail to capture the inherent uncertainty. The concept of multiple imputation (MI) is the same as simulation, that is, the unknown true value is replaced by multiple realizations of what the truth could be. Each realization of data is passed through the full modeling workflow to generate a realization of the geological model.
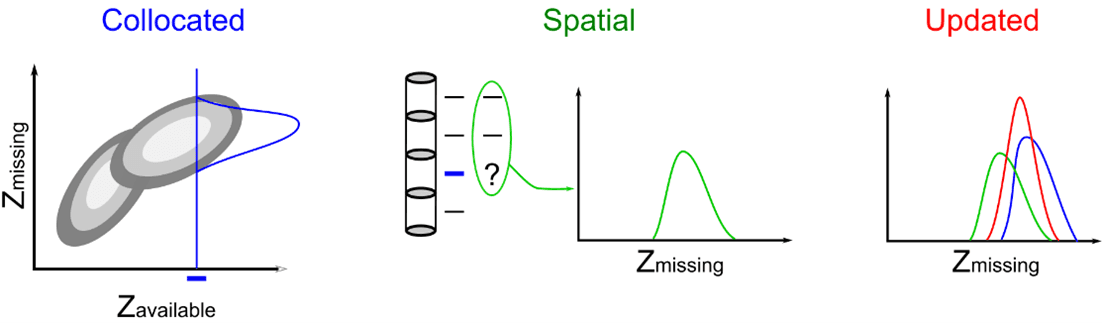
The schematic sketch illustrates the core steps in an MI algorithm for geological data: (1) calculate a conditional distribution given available collocated data (the blue distribution), (2) calculate another conditional distribution given spatial data of the same type (the green distribution), then (3) update or combine the distributions (the red distribution). An imputed value is drawn from the updated distribution. The imputation considers an outer loop over realizations (the MI concept), then a loop over all missing data locations.
Imputation is often applied to missing measurements due to either legacy sampling or geometallurgical samples that are expensive and not widely available. There are alternative applications. True values can be imputed given collocated measurements that contain error. Considering tabular deposits, position and thickness variables can be imputed for highly deviated drill holes.
The main point of this blog is to promote imputation, but there are situations when imputation is not the best technical solution. The main alternatives to imputation include (1) a form of cokriging that could be used to predict uncertainty with unequally sampled data, (2) the stepwise conditional transform (SCT) that requires a particular structure of missingness, but does not require a full valued data table, and (3) predicting the missing variable after geostatistical modeling of the variables that have been extensively sampled.
Cokriging should be considered when the sampling for all variables is quite extensive, but there are few samples that are collocated (homotopic). In this situation, cokriging can take advantage of the multivariate relationships, local data measurements and complex spatial features for improved local estimates. The SCT should be considered when there are exhaustive measurements of some variables over the area of interest or if some variables are always measured at the data locations; the variables later in the ordering of SCT must always have the earlier variables present. Finally, when some variables are very sparsely sampled, that is, there are less than (say) 100 measurements or less than (say) 5% of the database, then perhaps those variables should be predicted with some form of regression or machine learning after the extensively samples variables are predicted. This addresses the eternal question of whether to impute or not to impute.
Geological models should include all variables that influence decision making and geological models should be constrained to all available data. Resource Modeling Solutions (RMS) has the latest techniques implemented for either data imputation or the use the data without imputation.



